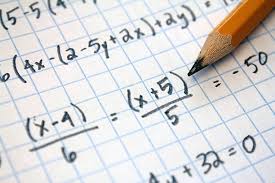Algebra คืออะไร ? ศาสตร์ของพีชคณิต

พีชคณิตคือสาขาพื้นฐานของคณิตศาสตร์ที่ต่อยอดจากเลขคณิต โดยใช้สัญลักษณ์ (ตัวแปร) แทนจำนวนที่ไม่ทราบค่า

เช่นตัวแปร X , Y

ซึ่งเด็กๆ ที่เรียนคณิตศาสตร์จำนวนมาก จะมีปัญหากับเรื่องสัญลักษณ์และตัวแปรเหล่านี้

เราใช้ พีชคณิตในการแก้ปัญหาในชีวิตประจำวัน โดยอาศัยหลักการ บวก , ลบ , คูณ , หาร ด้วยการสร้าง นิพจน์และสมการ เพื่อหาค่าที่ไม่ทราบ

โครงสร้างพีชคณิต (Algebraic structure)

หรือเรียกว่า ระบบพีชคณิต (algebraic system)

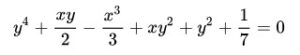
ตัวอย่างสมการ พีชคณิต

Axiom (สัจพจน์) คืออะไร?

Axiom (สัจพจน์) คือ ข้อความหรือข้อเสนอที่ได้รับการยอมรับว่าเป็นจริงโดยไม่ต้องมีการพิสูจน์ โดยถือเป็นจุดเริ่มต้นหรือรากฐานของระบบตรรกะหรือทฤษฎีใด ๆ ก็ตาม

• คุณสมบัติหลักของ Axiom:
  • เป็นจริงโดยตัวมันเอง: ไม่จำเป็นต้องมีเหตุผลหรือหลักฐานมาสนับสนุน
  • เป็นรากฐาน: ใช้เป็นหลักการพื้นฐานในการพิสูจน์ข้อความอื่น ๆ (ทฤษฎีบท) ที่ซับซ้อนขึ้น
  • ไม่ขัดแย้งกัน: ในระบบเดียวกัน สัจพจน์จะต้องไม่ขัดแย้งกันเอง

เปรียบเทียบง่ายๆ Axiom ก็เหมือนกับ “กฎพื้นฐาน” ของเกม เช่น ในกีฬาฟุตบอล กฎที่ว่า “ห้ามใช้มือสัมผัสลูกบอล” คือ Axiom อย่างหนึ่งที่ทุกคนต้องยอมรับเพื่อเล่นเกมได้

Axiom (สัจพจน์) ในทางคณิตศาสตร์คืออะไร?

ในทางคณิตศาสตร์ Axiom คือ ข้อความพื้นฐานที่ใช้เป็นรากฐานในการสร้างทฤษฎีทางคณิตศาสตร์ทั้งหมด โดยเป็นข้อความที่ถือว่าเป็นจริงโดยไม่มีการพิสูจน์ เพื่อใช้เป็นจุดเริ่มต้นในการให้เหตุผล (Deductive Reasoning) และพิสูจน์ทฤษฎีบท (Theorems) ต่างๆ ที่ตามมา

ระบบคณิตศาสตร์แต่ละสาขาจะถูกสร้างขึ้นจากสัจพจน์ชุดหนึ่งๆ ที่แตกต่างกันไป

ตัวอย่างสัจพจน์ในทางคณิตศาสตร์:

1. สัจพจน์ในเรขาคณิตแบบยุคลิด (Euclidean Geometry):
   • จากจุดสองจุดใดๆ สามารถลากเส้นตรงได้เพียงเส้นเดียว
   • สามารถลากเส้นตรงที่ต่อออกไปได้ไม่จำกัด
   • วงกลมสามารถวาดได้โดยมีจุดศูนย์กลางและรัศมีใดๆ ก็ได้
   • มุมฉากทุกมุมมีขนาดเท่ากัน
2. สัจพจน์ในทฤษฎีเซต (Set Theory) (ZFC Axioms):
   • Axiom of Extensionality: เซตสองเซตจะเท่ากันก็ต่อเมื่อมีสมาชิกเหมือนกันทุกประการ
   • Axiom of Empty Set: มีเซตว่างอยู่เสมอ
   • Axiom of Infinity: มีเซตของจำนวนธรรมชาติอยู่

ความสำคัญของ Axiom ในคณิตศาสตร์:

• สร้างความแม่นยำ: ช่วยให้การให้เหตุผลทางคณิตศาสตร์มีความแม่นยำและเป็นระบบ เพราะทุกการพิสูจน์จะอ้างอิงกลับไปยังสัจพจน์พื้นฐานที่ทุกคนยอมรับ
• เป็นรากฐานของทฤษฎี: ทฤษฎีบท (Theorems) ทั้งหมดในสาขาวิชาคณิตศาสตร์นั้นๆ จะต้องสามารถพิสูจน์ได้โดยอาศัยสัจพจน์ที่มีอยู่เท่านั้น
• นิยามระบบ: การเลือกสัจพจน์ที่แตกต่างกันจะนำไปสู่ระบบคณิตศาสตร์ที่แตกต่างกัน ตัวอย่างเช่น การเปลี่ยนแปลงสัจพจน์เรื่องเส้นขนานในเรขาคณิตยุคลิด นำไปสู่การเกิดของ เรขาคณิตแบบไม่ยุคลิด (Non-Euclidean Geometry) ซึ่งเป็นระบบคณิตศาสตร์ที่ถูกต้องอีกระบบหนึ่ง

โดยสรุปแล้ว Axiom คือ ข้อความที่ถือว่าเป็นจริงโดยไม่ต้องพิสูจน์ ซึ่งทำหน้าที่เป็นรากฐานและจุดเริ่มต้นในการสร้างทฤษฎีทางคณิตศาสตร์ที่ซับซ้อนยิ่งขึ้นต่อไป

ทำไมพีชคณิตจึงสำคัญ

• การสรุปเชิงหลักการ (Generalization): ช่วยให้นักคณิตศาสตร์สามารถทำงานกับแนวคิดที่กว้างและเป็นสากลได้ แทนที่จะจำกัดอยู่แค่ตัวเลขเฉพาะเจาะจงเท่านั้น ทำให้สามารถนำไปประยุกต์ใช้ได้ในสถานการณ์ที่หลากหลายมากขึ้น
• การแก้ปัญหา (Problem-Solving): พีชคณิตเป็นเครื่องมือที่เป็นระบบในการแสดงและแก้ปัญหาที่เกี่ยวข้องกับปริมาณที่ไม่ทราบค่า
• เชื่อมโยงไปสู่คณิตศาสตร์ขั้นสูง (Bridge to Higher Math): เป็นสะพานเชื่อมที่สำคัญระหว่างวิชาเลขคณิตขั้นพื้นฐานกับคณิตศาสตร์ขั้นสูง เช่น แคลคูลัส ตรีโกณมิติ และพีชคณิตนามธรรม (Abstract Algebra)
• การประยุกต์ใช้ในโลกแห่งความเป็นจริง (Real-World Applications): พีชคณิตถูกนำมาใช้เพื่อสร้างแบบจำลองและทำนายปรากฏการณ์ในโลกแห่งความเป็นจริง ตั้งแต่ความสัมพันธ์ระหว่างอุปทานและราคา ไปจนถึงวิถีการเคลื่อนที่ของลูกบอลที่ถูกขว้างออกไป

วิธีคิดเกี่ยวกับพีชคณิต

ลองคิดว่าพีชคณิตเป็นเครื่องมือที่ช่วยให้คุณตอบคำถามอย่าง

“จำนวนใด เมื่อนำมาบวกกับ 5 แล้วได้เท่ากับ 12?”

คำตอบคือ 7 และพีชคณิตจะช่วยให้คุณแสดงและหาคำตอบสำหรับค่าที่ไม่ทราบนี้ได้โดยใช้สัญลักษณ์ ตัวอย่างเช่น สมการ $x+5=12$ ใช้ตัวแปร $x$ แทนจำนวนที่ไม่ทราบ และเป้าหมายของการแก้สมการนี้คือการหาค่าของ $x$ ที่ทำให้ข้อความนี้เป็นจริง

แหล่งข้อมูลอ้างอิง

Wikipedia : Algebra

Wikipedia : Algebraic structure

ท่านที่สนใจเรียนคณิตศาสตร์ สามารถศึกษารายละเอียดเพิ่มเติมได้ที่ คอร์สเรียนคณิตศาสตร์ โดยสถาบัน RedSiam